These are the ramblings of Matthijs Kooijman, concerning the software he hacks on, hobbies he has and occasionally his personal life.
Most content on this site is licensed under the WTFPL, version 2 (details).
Questions? Praise? Blame? Feel free to contact me.
My old blog (pre-2006) is also still available.
See also my Mastodon page.
- Raspberry pi powerdown and powerup button (45)
- Repurposing the "Ecobutton" to skip spotify songs using Linux udev/hwdb key remapping (3)
- How to resize a cached LVM volume (with less work) (2)
- Reliable long-distance Arduino communication: RS485 & MODBUS? (6)
- USB, Thunderbolt, Displayport & docks (21)
| Sun | Mon | Tue | Wed | Thu | Fri | Sat |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 |
(...), Arduino, AVR, BaRef, Blosxom, Book, Busy, C++, Charity, Debian, Electronics, Examination, Firefox, Flash, Framework, FreeBSD, Gnome, Hardware, Inter-Actief, IRC, JTAG, LARP, Layout, Linux, Madness, Mail, Math, MS-1013, Mutt, Nerd, Notebook, Optimization, Personal, Plugins, Protocol, QEMU, Random, Rant, Repair, S270, Sailing, Samba, Sanquin, Script, Sleep, Software, SSH, Study, Supermicro, Symbols, Tika, Travel, Trivia, USB, Windows, Work, X201, Xanthe, XBee
 &
&
(With plugins: config, extensionless, hide, tagging, Markdown, macros, breadcrumbs, calendar, directorybrowse, feedback, flavourdir, include, interpolate_fancy, listplugins, menu, pagetype, preview, seemore, storynum, storytitle, writeback_recent, moreentries)
Valid XHTML 1.0 Strict & CSS
It has been a while since my last post on this subject, unfortunately this is related to my own lack of activity in this area. I've been too busy with other courses and non-study related stuff in the past weeks.
Since the deadline for the peer reviews of my paper is next Friday, I have put my Bachelor Referaat at the top of my priority list, very lonely. With good results. So far I've made a structure with some general content (Introduction, something about LocSim, etc). I've been finishing up on the obstacle thing in LocSim. Most algorithms should now work with obstacles. I've implemented my improvement and got actual, measurable, results!
Initial testing was a bit weird, since some quick test cases showed that, regularly, adding obstacles to the equation made normal localization perform better instead of worse. Some of this was caused by simple algorithm I used for testing (Centroid). In many cases, it could not determine any position at all, resulting in NaN's in the computed positions. The block that determines the average error simply discarded these. So, if an obstacle would make the worst guesses no guess at all, average performance would increase... Stuff is getting better, though.
Yesterday, I managed to get Matlab working on Linux too, which saves me a lot of reboots (Before I only had Matlab in Windows, while the LaTeX environment to write was in Linux...). I managed to get my hands on a copy of Matlab with proper 64bit support, all previous versions had that crucial bit removed... Installing was a breeze, I've not encountered any real issues yet.
I'm getting a bit more comfortable in Matlab too, finding out where different features are to be found and how the programming language works. I might actually say I like it, so far.
Algorithm
I've decided to use a range based algorithm to improve with my idea. Originally, I wanted to try a few algorithms and improvements, but time constraints have changed my mind here. Range based algorithm are algorithms that use distance guesses based on, for example, radio signal strength in their calculation (Opposed to range free algorithms that only use the fact that two nodes can hear each other or not). I expect that range based algorithms will have more trouble coping with obstacles, I will use these (though I can't really provide solid argumentation for this on such short notice...).
My algorithm of choice, being the simplest range based algorithm, is DvDistance. Essentially each node just makes an educated guess of the distance to each anchor in the system, by adding range estimations of all 'hops' on the shortest path to the anchor together. Also, it finds out where each of these anchors are located in reality. Lastly, it will just try different locations. For each location, it can calculate the distance to each of the anchors. Now comparing these calculated distances to the guessed distances above (using the least-squares method) gives a value for the error in the position we tried. Simply trying a lot different positions and taking the one that gives the smallest error is all that is left.
Algorithm Improvement
So, how to improve on this? The theory is that, in the face of obstacles, localization will be offset away from the obstacle (since the obstacle makes the range estimation higher than they really are). So, to get better results, we should correct our calculated position towards the obstacle. But, how much? And which way? How do we even know there is an obstacle?
Here the anchors come in. We let the anchors perform the same localization, as if they were normal nodes. Since the anchors know where they are, they can calculate how much the algorithm is off. Nodes in the neighbourhood now correct for this error and hope they will get better results.
This is how (part of this) looks like in Matlab:
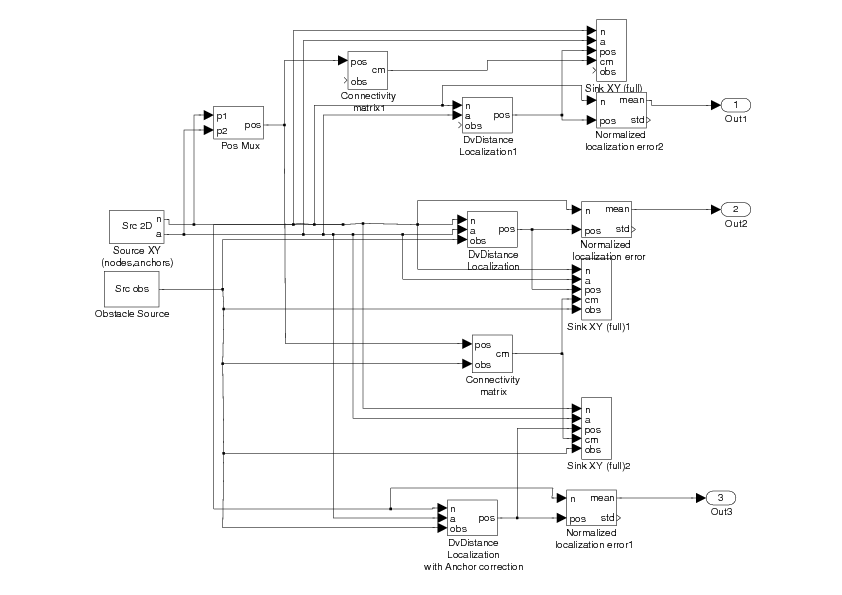
Example
While debugging, I made a small test case, that I had also used in my research proposal. After some tweaking and bug fixing, this example illustrated the intended effect very nicely. The example situation, with no obstacles or improvements was quite simple.
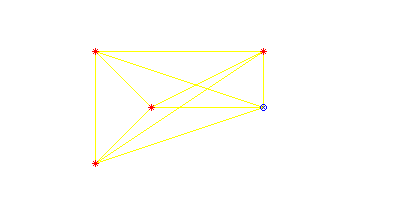
In this figure, the red stars are the anchors, the black cross is a single node, and the circle is where the node thinks it is. Yellow lines are nodes that can hear each other. As you can see, localization is perfect here, since the node can hear three different anchors directly.
In the next figure, I've put a giant wall in the middle.
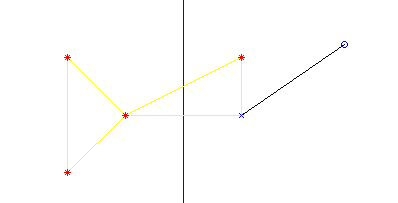
As you can see, the node doesn't quite where it is now. It's position is way too far to the right, due to the wall making the anchors on the left seem farther away than they really are.
In this last figure, I have applied my improvement.
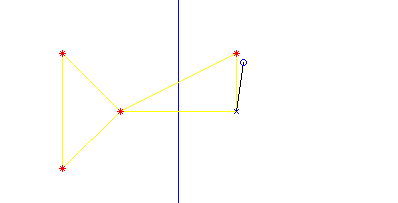
Here, the anchor to the right experiences a similar offset as the node, and correcting that offset reduces the error significantly. There is still quite some error left, which is also related to the fact that the node bases its localization on 4 anchors, while the anchor only uses the other 3.
Results
Though I am enthousiastic about this research, I have mostly expected to come back empty-handed, probably even with an improvement that would make things worse. So far, results seem more promising than expected.
Initial testing using a single obstacle in the middle of the area (separating the area in two) shows an average error of around 0.1, 0.5, 0.2, respectively the error without obstacles, with obstacles and with obstacles and correction. In other words, this is an improvement of 60%!
Some more testing with random obstacles (length 30% of the area size) shows that improvement is a lot less (0.09, 0.12, 0.11 IIRC). Increasing the length of the obstacles to 70% also increases the improvements (can't remember values).
To cut a long story short, my improvement is actually working! No, I need to get back to it, since I still need to write a paper about it. Perhaps I should just put a link to my blog in there...

Comments are closed for this story.